End-to-End Structure Solutions from Information-Compromised Diffraction Data via Generative Deep Learning

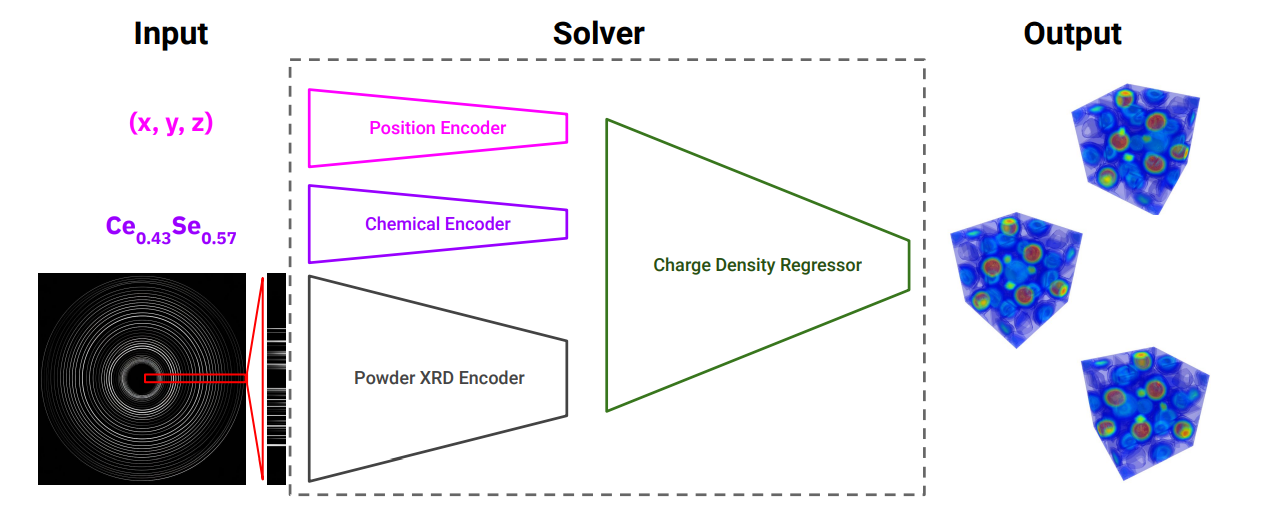
The revolution in materials in the past century was built on a knowledge of the atomic arrangements and the structure-property relationship. The sine qua non for obtaining quantitative structural information is single crystal crystallography. However, increasingly we need to solve structures in cases where the information content in our input signal is significantly degraded, for example, due to orientational averaging of grains, finite size effects due to nanostructure, and mixed signals due to sample heterogeneity. Understanding the structure property relationships in such situations is, if anything, more important and insightful, yet we do not have robust approaches for accomplishing it. In principle, machine learning (ML) and deep learning (DL) are promising approaches since they augment information in the degraded input signal with prior knowledge learned from large databases of already known structures. Here we present a novel ML approach, a variational query-based multi-branch deep neural network that has the promise to be a robust but general tool to address this problem end-to-end. We demonstrate the approach on computed powder x-ray diffraction (PXRD), along with partial chemical composition information, as input. We choose as a structural representation a modified electron density we call the Cartesian mapped electron density (CMED), that straightforwardly allows our ML model to learn material structures across different chemistries, symmetries and crystal systems. When evaluated on theoretically simulated data for the cubic and trigonal crystal systems, the system achieves up to 93.4% average similarity with the ground truth on unseen materials, both with known and partially-known chemical composition information, showing great promise for successful structure solution even from degraded and incomplete input data. The approach doesn’t presuppose a crystalline structure and the approach are readily extended to other situations such as nanomaterials and textured samples, paving the way to reconstruction of yet unresolved nanostructures.

For more details, checkout the npj Computational Materials paper, and view the code.